Sequence and Series – Definition, Types, Examples
In this article, we look at Sequences and Series – definition, types and Worked Examples.
Douglas Tawiah Dwumor

[Sassy_Social_Share title="Sharing is Caring" count="1" total_shares="ON"]
- Sequence is a set of ordered numbers
- Finite sequence ends. Infinite sequence continues to infinity.
- Series is when the terms in a sequence are connected by +ve or -ve or both
RECOMMENDED ARTICLES
Permutation – Definition, Formula, Practical Examples
In this article, we look at Permutation - definition, types and examples. [Sassy_Social_Share title="Sharing is Caring" count="1" total_shares="ON"] Permutation is the arrangement of items in order Given n number of items, r items can be permutated where $r \le n$....
Finding the position number of a term and number of terms in Arithmetic Progression
In this article, we look at how you can determine the position number of a term in an Arithmetic Progression (A.P.) or Linear Sequence. [Sassy_Social_Share title="Sharing is Caring" count="1" total_shares="ON"] Given common difference, first term the position number...
Sets and Operations on Sets
[toc]
A sequence is a set of numbers (or terms) arranged in a defined order such that there is a rule for obtaining the numbers. For example, $1,2,3,4,5,…$ is a sequence of numbers. We observe that each succeeding term increases by 1. That’s, we can obtain terms in the sequence by adding 1 to the preceding term. The Sequence can be descending too. For example, $45, 41, 37, 33, 29,…$ is a sequence.
Finite and Infinite Sequence
A finite sequence is a type of sequence whose last term is known. For example, $2,4,6,8,10$ is a finite sequence. The last term is 10.
Infinite Sequence
Infinite Sequence is a type of sequence whose last term is not known. For example, $2,4,6,8,10,…$ is an infinite sequence..The three dots (…) indicate the sequence continues to infinity.
Series
A series is formed when the terms in a sequence are connected by either +ve or -ve or both. For example, $1+2+3+4+5+…, 1+2-3+4-5+6-7…$ are series.
Finite and Infinite Series
A finite series is a type of series whose last term is known. For example, $2+4+6+8+10$ is a finite series. The last term is 10.
Infinite Series
Infinite Series is a type of series whose last term is not known. For example, $2,4,6,8,10,…$ is an infinite series..The three dots (…) indicate the series continues to infinity.
Types of Progression
We will consider five types of progressions. These are Arithmetic Progression (A.P.), Geometric Progression (G.P.), Arithmetico-Geometric progression (AGP), Harmonic Progression (H.P.) and Fibonacci Sequence.
Arithmetic Progression (A.P)
An Arithmetic Progression is a progression where the algebraic difference between any two consecutive terms is constant or the same throughout. For example, $3, 5, 7, 9, …$ is an Arithmetic Progression (A.P.). The constant difference between any two consecutive terms is 2. This is called the common difference.
An A.P. is also called a linear sequence. This is because the constant difference between consecutive terms in an A.P. creates a straight line when plotted on a graph, hence the term “linear.”
In other words, the relationship between the terms in an AP can be represented by a linear equation of the form $y=mx+c$, where
$m$ represents the common difference (slope) between consecutive terms, and
$c$ represents the initial term (y-intercept).
Terms in an A.P.
Let $U_n$ represent a term in an A.P. Thus, U1 is first term, $U_2$ is second term, $U_3$ is third term etc.
$U_n$ is any term where $n≥1$. $U_n$ is called the $nth$ term. This means when $n=1$, we have $U_1$, first term. When $n=2$, we have $U_2$, second term.
The first term in an A.P. , $U_1$, is normally represented by $a$. That’s, $U_1=a$.
$=> U2= a + d$
$U3= a + d + d = a+2d$
$U4 = a + d + d + d=a+3d$
$U5= a + d + d + d + d = a+4d$
$U6= a + d + d + d + d +d= a+5d$
$\vdots$
$Un= a + (n-1)d$
We observe that the first term ($U_1$) has zero $d$, the second term ($U_2$) has 1 $d$. The third term ($U_3$) has $2d$, as in $U_2=a+2d$; the fourth term ($U_4$) has $3d$, as in $a+3d$. This implies that $U_n$ term will have (n-1) $d$. That’s, $U_n=a +(n-1)d$.
The general term for obtaining the terms in an Arithmetic Progression or linear Sequence is
$U_n = a + (n-1)d$
where
$n$=position number of a term and n≥1
$a$=first term
$d$=common difference (between consecutive terms)
The Common Difference (d)
The common difference is obtained by subtracting a preceding term from a consecutive term. For example, given the sequence $2,4,6,8,10,…$
$d=4-2$ or $6-4$ or $8-6$ or $10-8$ etc
Therefore, $d=U_2-U_1$ or $U_3-U_2$ or $U_4-U_3$ … $U_n -U_{n-1}$ or $U_{n+1} – U_n$.
Finding a term in an A.P.
Example 1:
Find the 9th term of the Arithmetic Progression (A.P.) $3,7, 11, 15,…$
Solution
The Sequence is $3,7, 11, 15,…$
First term (a)=3
common difference (d)$= 7-3=4$
position number of term (n) = 9 [Note: 9th term]
The general term (nth term) of an A.P. is given by
$U_n = a + (n-1)d$
$U_9= 3 + (9-1)(4)$
$= 3 + (8)(4)$
$= 3 + 32$
$=35$
Example 2:SSSCE July 2002 OBJ Q5
A sequence is given as $-5,-2,1,4,…$. Find the $23rd$ term.
Solution
The Sequence is $-5,-2,1,4,…$
First term (a)$=-5$
common difference (d)$= -2-(-5)=3$
position number of term (n) = 23 [Note: 23rd term]
The general term (nth term) of an A.P. is given by
$U_n = a + (n-1)d$
$U_9= -5 + (23-1)(3)$
$= -5 + (22)(3)$
$= -5 + 66$
$=61$
Example 3: SSSCE July 2003 OBJ Q19
Write down the 27th term of the sequence 1951, 1954, 1957, 1960 …
Solution
The Sequence is $1951, 1954, 1957, 1960 … $
First term (a)$=1951$
common difference (d)$= 1954-1951=3$
position number of term (n) = 27
The general term (nth term) of an A.P. is given by
$U_n = a + (n-1)d$
$U_9= 1951 + (27-1)(3)$
$= 1951 + (26)(3)$
$= 1951 + 78$
$=2029$
Example 4: WASSCE Nov 2014 OBJ Q8
Find the $26th$ term of the sequence $1909, 1913, 1917, 1921…$.
Solution
The Sequence is $1909, 1913, 1917, 1921… $
First term (a)$=1909$
common difference (d)$= 1913-1909=4$
position number of term (n) = 26
The general term (nth term) of an A.P. is given by
$U_n = a + (n-1)d$
$U_9= 1951 + (26-1)(4)$
$= 1909 + (25)(4)$
$= 1909 + 100$
$=2009$
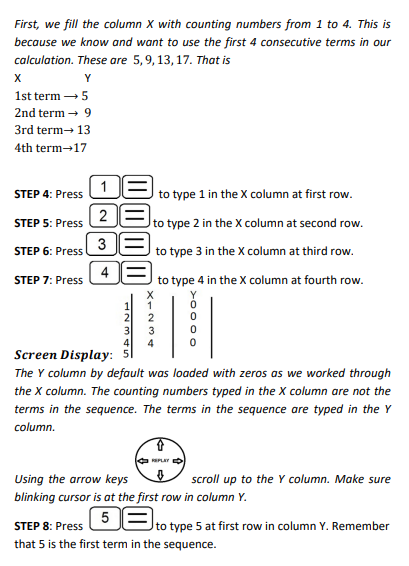
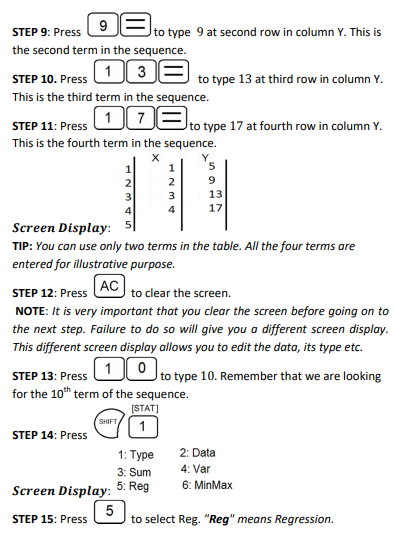
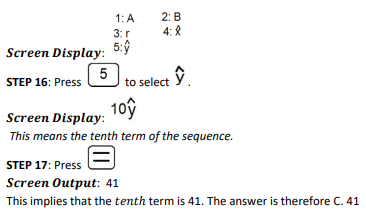
Technology (Using the Scientific Calculator)

You May Also Like…
Permutation – Definition, Formula, Practical Examples
In this article, we look at Permutation - definition, types and examples. [Sassy_Social_Share...
Finding the position number of a term and number of terms in Arithmetic Progression
In this article, we look at how you can determine the position number of a term in an Arithmetic...



0 Comments