Rectangular Coordinate System
In this article, we look at how to draw the x-y coordinate system, identify the quadrants of the coordinate system, plot points in the x-y coordinate system.
Douglas Tawiah Dwumor

- Learn to create a coordinate plane
- Learn to plot an ordered pair in the coordinate plane.
- Learn to find the quadrant in which an ordered pair lies.
RECOMMENDED ARTICLES
No Results Found
The page you requested could not be found. Try refining your search, or use the navigation above to locate the post.
Cartesian Coordinate System
The Cartesian Coordinate System is another name for a rectangular coordinate plane. This plane lets us plot ordered pairs and graph linear equations with two variables. It may also be called the coordinate plane, the coordinate system, or the Cartesian coordinate plane. In this course, we will usually call it the coordinate plane.
To draw the coordinate plane, we set up two number lines. The x-axis is the horizontal line, which shows x-values. The y-axis is the vertical line, which shows y-values. Let’s look at the coordinate plane:
The point where the x-axis and y-axis meet is called the origin. At the origin, both the x-value and y-value are 0, written as (0,0).
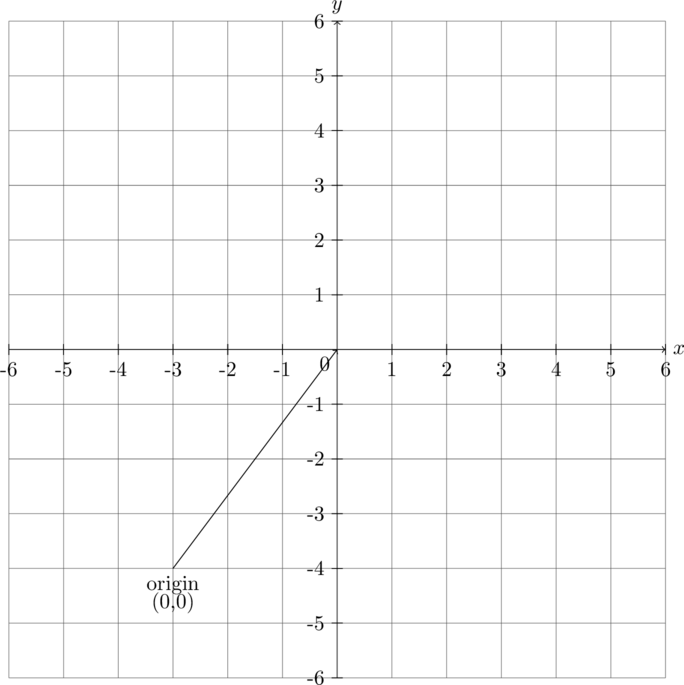
On the horizontal number line (x-axis), numbers increase to the right and decrease to the left. On the vertical number line (y-axis), numbers increase upwards and decrease downwards.
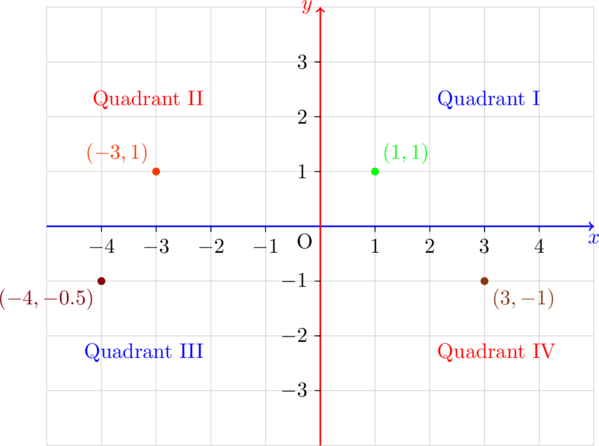
The coordinate plane is divided into four quadrants labeled with Roman numerals: I, II, III, and IV. Quadrant I is in the upper right, and the others follow counterclockwise.
Points on the x-axis or y-axis do not belong to any quadrant.
Quadrant I: (+, +)
Quadrant II: (-, +)
Quadrant III: (-, -)
Quadrant IV: (+, -)
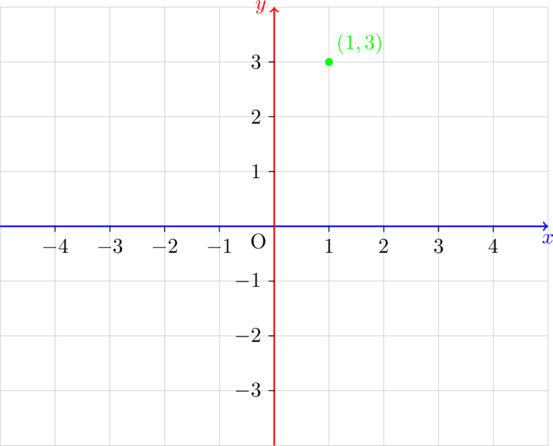
How to plot a point on Cartesian Plane
We often call an ordered pair a “point.” To plot a point (an ordered pair), we start at the origin (0,0).
- Here’s how to do it:
Move right or left on the x-axis for the x-value. - Move up or down on the y-axis for the y-value.
For example, to plot the point (1,3 ):
- Move 1 unit to the right from the origin on the x-axis.
- Then move 3 units up from the x-axis.
At this spot, mark a filled-in circle to represent the point (1, 3).
Review Exercises
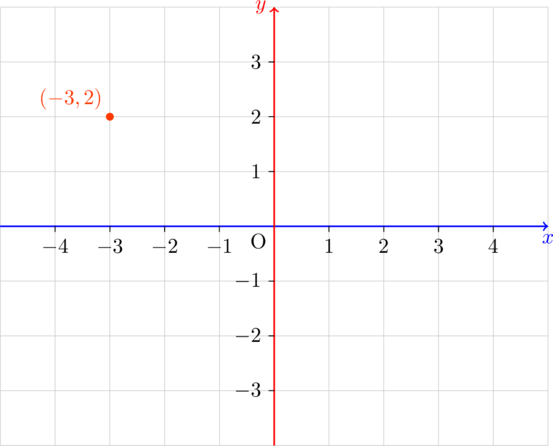
Example 1: Plot the point ![]() and determine its quadrant.
and determine its quadrant.
You May Also Like…
No Results Found
The page you requested could not be found. Try refining your search, or use the navigation above to locate the post.

0 Comments